The mathematical relationship between pressure and the number of moles is a simple gas law.

The Relationship Between Pressure and Number of Moles

Definition
Formulas
Example
Video
Exercise

Other Simple Gas Laws

The relationship between pressure |(P)| and the number of moles |(n)| describes the relationship between those two variables when the volume |(V)| and the temperature |(T)| are constant.

Consider a certain amount of gas in an incompressible container at constant temperature.

A closed container with a given amount of gas. The particles of gas apply pressure on the container walls. This pressure is measured by a manometre.

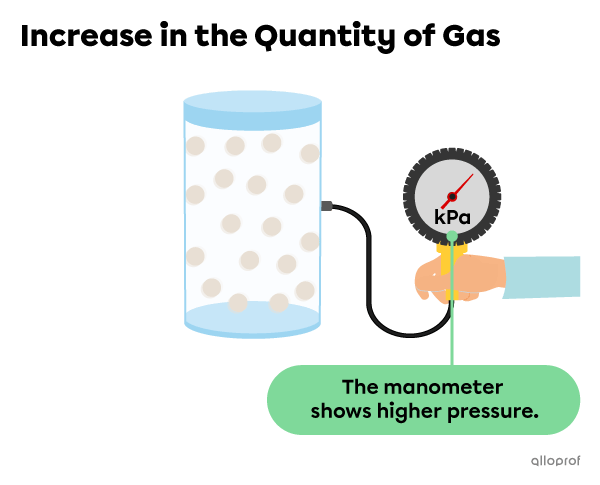
If the amount of gas in the container increases, the particles become more squeezed together, resulting in more collisions. This leads to greater pressure on the walls of the container.

A closed container with a given amount of gas. The particles of gas apply pressure on the container walls. This pressure is measured by a manometer. When the number of particles increases, the number of collisions also increases, leading to greater pressure on the walls of the container.

If the amount of gas in the container decreases, the particles become less squeezed together, resulting in less collisions. This leads to lower pressure on the walls of the container.

In short, when the temperature |(T)| and the volume |(V)| are constant, as the amount of gas increases, the pressure increases. Inversely, as the amount of gas decreases, the pressure decreases.

A graph showing that the relationship between the pressure of a gas and the number of moles is an oblique line passing through the y-coordinate at the origin.

This graph describes the direct variation between the pressure of a gas and the number of moles.

The pressure of a gas is directly proportional to its number of moles. This relationship can be expressed using the following formula.

When |V| and |T| are constant:

|P\propto n| or |\dfrac{P}{n}=\text{constant}|
where
|P : | pressure often in kilopascals |(\text{kPa})|
|n : | quantity of gas in moles |(\text{mol})|

We can also compare an initial situation with a final situation in which the pressure and the number of moles of a gas have changed by using the following formula.

When |V| and |T| are constant:

|\dfrac{P_1}{n_1} = \dfrac{P_2}{n_2}|
where
|P_1 : | initial pressure often kilopascals |(\text{kPa})|
|n_1 : | initial quantity of gas in moles |(\text{mol})|
|P_2 : | final pressure often in kilopascals |(\text{kPa})|
|n_2 : | final quantity of gas in moles |(\text{mol})|

Be careful!

Simple gas laws apply only for ideal gases.

The values calculated using the simple gas laws correspond approximately to the real values, as long as the gas temperature is not too low and the pressure is not too high.

A car tire is punctured. Initially, the air pressure in the tire is |220\ \text{kPa}| and the amount of gas is |0{.}898\ \text{mol}.| After a while, |0{.}122\ \text{mol}| of air escaped from the tire.

What is the final air pressure in the tire?

The volume of the tire and the temperature are assumed to be constant.

See solution

Video

Video coming soon!

Exercise

Exercise coming soon!

The Relationship Between Pressure and Number of Moles