The Logarithmic Function
The logarithmic function is the inverse of the exponential function. It is a function which consists of a vertical asymptote where the domain is restricted.
When working with a logarithmic function, several laws and calculations specific to logarithms are used. Other related concepts can also be reviewed.
Related concepts
- The Basic Logarithmic Function
- The Transformed Logarithmic Function
- The Role of the Parameters in a Logarithmic Function
- Graphing the Logarithmic Function
- Finding the Rule of a Logarithmic Function
- The Properties of a Logarithmic Function
- Solving Problems Involving the Logarithmic Function
- The Inverse of the Logarithmic Function
The Basic Logarithmic Function
The rule of the basic logarithmic function is |f(x)=\log_cx| where |c\neq 1| and |c>0.|
The logarithm’s argument |(x)| must be greater than |0.|
-
The basic logarithmic function moves closer and closer to the y-axis, without ever touching it. The y-axis therefore corresponds to a vertical asymptote.
-
The basic logarithmic function has a zero, but no y-intercept.
-
The points of the function are all located to the right of the asymptote. Therefore, its domain is over the interval |]0,\infty[.|
-
When |\color{#333FB1}{c>1},| the function is increasing.
-
When |\color{#3A9A38}{0<c<1},| the function is decreasing.

Important!
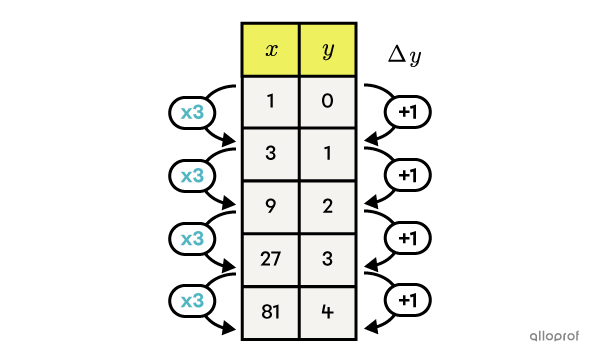
In a logarithmic function, the independent variable is the power and the dependent variable is the exponent. Therefore, when the dependent variable (the exponent) increases by one unit, the independent variable (the power) varies by a factor of |\color{#51B6C2}c.|
The following is an example with the function |f(x)=\log_\color{#51B6C2}3x|
||\begin{align}f(x)&=\log_\color{#51B6C2}3x\\0& =\log_\color{#51B6C2}3(1)\\1&=\log_\color{#51B6C2}3(3)\\2&=\log_\color{#51B6C2}3(9)\\3&=\log_\color{#51B6C2}3(27)\\4&=\log_\color{#51B6C2}3(81) \\&\quad\cdots\end{align}||
The 2 bases most often used are base |10| and base |e.|
Base |\boldsymbol{10}| Logarithm
A logarithm with base |10| is simply written without its base. The base |10| logarithm is often used to perform calculations using the calculator, which is in base |10.|
|\log_{10}x=\log x|

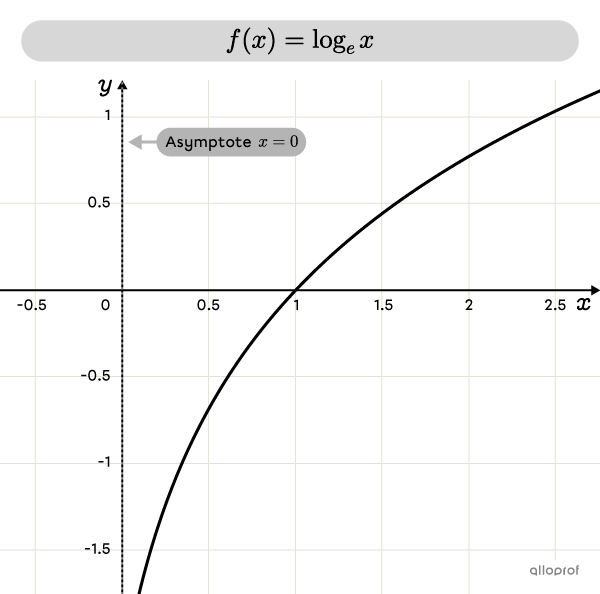
Base |\boldsymbol{e}| Logarithm
The base |e| logarithm is called the natural logarithm. The number |e,| called Euler's Number, is an irrational number, that is, it has a non-repeating and infinite expansion.
|\log_e x=\ln x| where |e\approx 2.72|
The transformed logarithmic function
There are 2 types of rules when the logarithmic function is transformed.
The form |\boldsymbol{f(x)=a\log_c(bx)}|
where
|a\neq 0,| |b\neq 0,| |c\neq 1,| |c>0|
and
|x=0| corresponds to the equation of the vertical asymptote.
The logarithm’s argument |(bx)| must be greater than |0.|
The form |\boldsymbol{f(x)=a\log_c\big(b(x-h)\big)+k}|
where
|a\neq 0,| |b\neq 0,| |c\neq 1,| |c>0|
and
|x=h| corresponds to the equation of the vertical asymptote.
The logarithm’s argument |\big(b(x-h)\big)| must be greater than |0.|
